Best IoU Loss for Bounding Box Regression
Published:
Introduction
Object Detection consists of two sub-tasks: Object Localization and Object Classification. The common goal of object localization is to determine coordinates of objects in the picture.
Bounding box regression is crucial step to determine objects. In existing methods, the common cost functions of bounding box regression are used by $l_n-norm$ distance and IoU for evaluating metric. Currently, IoU loss, GIoU loss, DIoU loss, … have been proposed to benefit the IoU metric, achieving faster convergence and make the regression more accurate.
Generalized Intersection over Union (GIoU)
The IoU value is computed based on ground-truth box and predicted box. During training model, the cost function is usually optimized to return the best of predicted box and compute IoU to evaluate model. The below example show that if we calculate $l1-norm$ and $l2-norm$ distance for bounding boxes in cases, the $l_n-norm$ values are exactly the same, but their IoU and GIoU values are very difference. Therefore, there is no strong relation between loss optimization and improving IoU values.
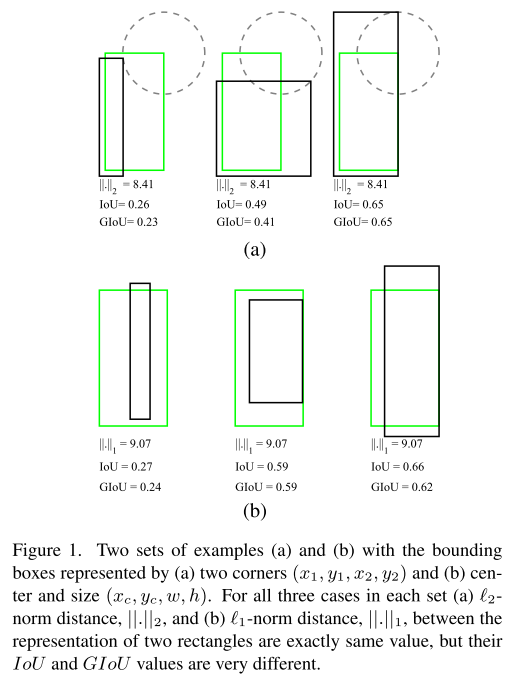
Generalized version of IoU can be directly used as the objective function to optimize in the object detection problem. When IoU does not reflect if two shapes are in vicinity of each other or very far from each other.
\[GIoU = IoU - \frac{\mid C\setminus {(A\cup B)}\mid}{\mid C \mid}\]Cost function for bounding box regression:
\[L_{GIoU} = 1-GIoU\]Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression (DIoU)
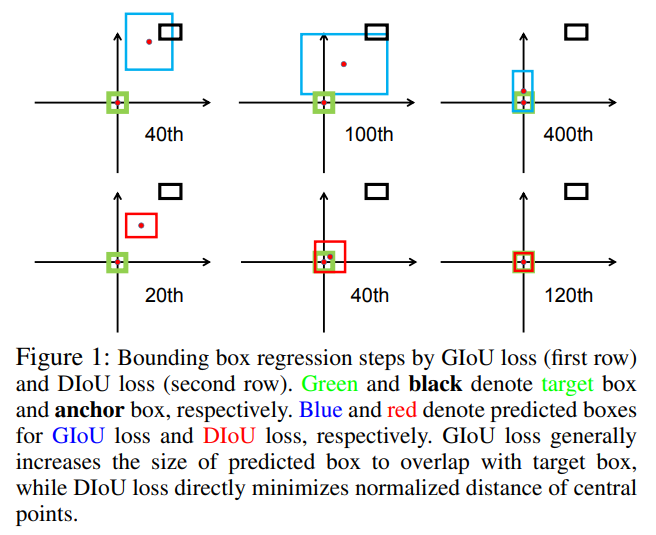
In the paper, the author provides three typical cases in simulation experiments:
First, the anchor box is set at a diagonal orientation. GIoU loss tends to increase the size of the predicted box to overlap with the target box, while DIoU loss directly minimizes the normalized distance of centre points
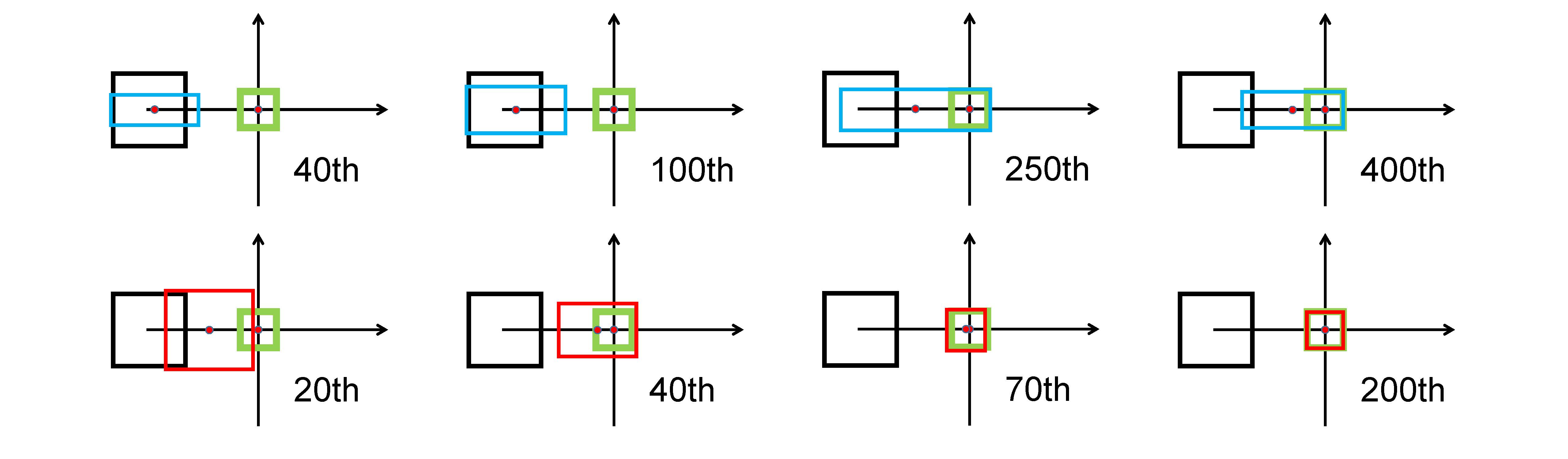
Second, the anchor box is set at the horizontal orientation. GIoU loss broadens the right edge of the predicted box to overlap with the target box, while the central point only moves slightly towards the target box. On $th$ other hand, from the result at $T=400$, GIoU loss has totally degraded to IoU loss, while DIoU loss only at $T=120$
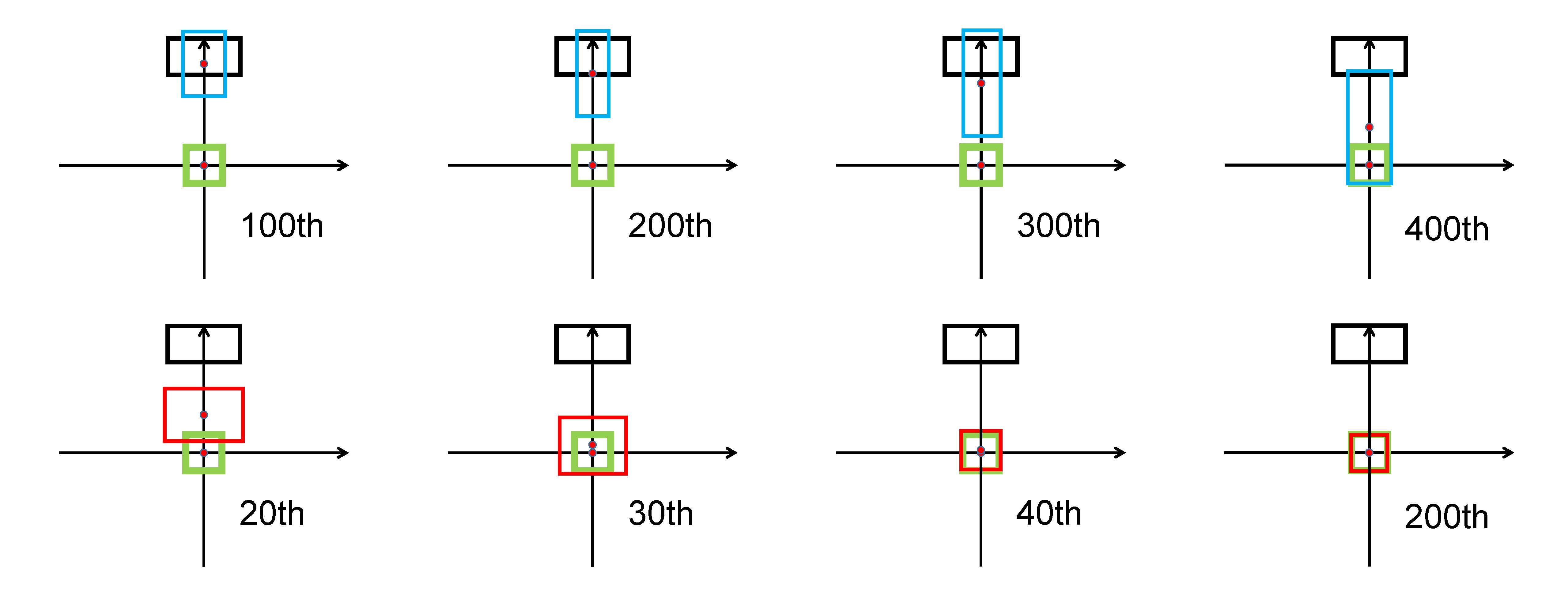
Third, the anchor box is set at the vertical orientation. Similarly, GIoU loss broadens the bottom edge of the predicted box to overlap with the target box and these two boxes do not match in the final iteration.
To minimize the normalized distance between central points of two bounding boxes, and the penalty term can be defined as
\[R_{DIoU}=\frac{\rho^2 (b, b^{gt})}{c^2}\]where $b$ and $b^{gt}$ denote the central points of $B$ and $B^{gt}$, $\rho(.)$ is the Euclidean distance, and $c$ is the diagonal length of the smallest enclosing box covering the two boxes. And then the DIoU loss function can be defined as
\[L_{DIoU}=1 - IoU + \frac{\rho^2 (b, b^{gt})}{c^2}\]Complete IoU Loss (CIoU)
DIoU aswerd the question: Is it feasible to directly minimize the normalized distance between predicted box and target box for achieving faster convergence?, CIoU will answer the question: How to make the regression more accurate and faster when having overlap even inclusion with target box?
CIoU is a good loss for bounding box regression consider three important geometric factors (overlap area, central point distance and aspect ratio).
There fore, based on DIoU loss, the CIoU loss is proposed by imposing the consistency of aspect ratio.
\[R_{CIoU} = \frac{\rho^2(b, b^{gt})}{c^2} + \alpha v\]where $\alpha$ is a positive trade-off parameter, and $v$ measures the consistency of aspect ratio.
\[v=\frac{4}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})^2\] \[\alpha = \frac{v}{(1-IoU)+v}\]The loss function can be defined as
\[L_{CIoU}=1-IoU + \frac{\rho^2(b, b^{gt})}{c^2} + \alpha v\]