Core Probability
Published:
Why Probability
Anything that happens in our life is uncertain. There’s uncertainty anywhere so whatever you try to do, you need to have some way of dealing or thinking about uncertainty. And the way to do that in a systematic way is using the models that are given to us by Probability Theory. So if you’re an engineer and you’re dealing with some real-world problems. Basically, you’re facing I wonder if the crush loves me, it is random, is uncertain. So, how do you model it? how to you deal with it?
1. Core Probability and Aximos
Sample space ($\Omega$): is the set of all possible outcomes of an experiment.
- Discrete: $\Omega = \lbrace 1, 2, 3, 4, … \rbrace$
- Continuous: $\Omega = \lbrace(x, y)\vert 0 <= x, y <= 1 \rbrace$
Probaility Aximos
The probability of any event $E$ can be defined as:
\[P(E) = \lim_{n \rightarrow \infty} \frac{\text{count}(E)}{n}\]Nonegativity:
\[0 \leq P(E) \leq 1\]All outcomes must be from the Sample Space:
\[P(\Omega)=1\]The probability of an event from its complement:
\[P(E) = 1 - P(E^c)\]Probability of or with Mututally Exclusive Events:
\[E_1 \cap E_2 = \varnothing => P(E_1 \cup E_2)=P(E_1) + P(E_2)\]If $E_1, E_2, …, E_n$ are disjoint sets (mutually exclusive)
\[P(E_1 \cup E_2 \cup .... \cup E_n) = P(E_1) + P(E_2) + ... + P(E_n)=\sum_{i=1}^{n}P(E_i)\]Probability of or (Inclusion-Exclusion):
\[P(E_1 \cup E_2) = P(E_1) + P(E_2) - P(E_1 \cap E_2)\]Probability of and for independent events: If events are independent, the probability of two events occurring is
\[P(E_1 \cap E_2 ... \cap E_n) = \prod_{i=1}^{n}P(E_i)\]General Probability of and (The Chain Rule):
\[P(E_1 \cap E_2 ... \cap E_n) = P(E_1). P(E_2 \vert E_1). P(E_3|E_1 \cap E_2) ... P(E_n|E_1\cap ... \cap E_{n-1})\]The Law of Total Probability: For an event $E$, if you can divide the sample space into any number of mutually exclusive events: $B_1, B_2, …, B_n$:
\[P(E) = P(E \cap B_1) \cup P(E \cap B_2) \cap ... \cap P(E \cap B_n) = \sum_{i=1}^n P(E \cap B_i)\]Bayes’ Theory
\[P(B\vert E) = \frac{P(E\vert B). P(B)}{P(E)}\]
1.1 Counting
Definition: Step Rule of Counting (aka Product Rule of Counting)
If an experiment with two parts, $A$ is the first part, $B$ is the second part (the outcomes in $B$ is regardless of the outcomes of $A$): \(\vert A \vert=m, \vert B \vert=n\)
The total number of outcomes for the expepriment:
\[\vert A \vert . \vert B \vert = m.n\]Counting with or
Mutually Exclusion Counting: $A \cap B = \varnothing$, the possible outcomes of the experiment
\[\vert A \cup B \vert = \vert A \vert + \vert B \vert\]Inclusion Exclusion Counting: $A \cap B \neq \varnothing$, the possible outcomes of the experiment.
\[\vert A \cup B \vert = \vert A \vert + \vert B \vert - \vert A \cap B \vert\]1.2 Combinatorics
Permutations of Distinct Objects
Permutation Rule: A permutation is an ordered arrangement of $n$ distinct object. Those $n$ object can be permuted in $m$ ways \(m = n.(n-1).(n-2)... 2. 1 = n !\)
Permutations of Indistinct Objects
Generally when there are $n$ objects and:
$n_1$ are the same and $n_2$ are the same … $n_k$ are the same.
The number of distinct permutation is:
\[m = \frac{n!}{n_1!n_2!...n_k!}\]Combinations of Distinct Objects
A combination is an unordered selection of $k$ objects from a set of $n$ objects
\[m=\frac{n!}{k!(n-k)!} = \left( \begin{array}{c} x \\ y \end{array} \right)\]1.3 Probability of or
Or with Mutually Exclusive Events: For $n$ events $E_1, E_2, …, E_n$ where each event is mutually exclusive of one another:
\[P(E_1 \cup E_2 \cup ... \cup E_n) = P(E_1) + P(E_2) + ... + P(E_n) = \sum_{i=1}^n P(E_i)\]Or with Non-Mutually Exclusive Events
- For 2 any events $E_1, E_2$:
- For 3 events: $E_1, E_2, E_3$
1.4 Conditional Probability
Conditional Probabilty
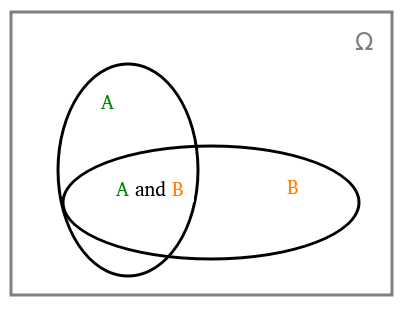
$P(A\vert B)$ : The probability of $A$ given that $B$ occured
Assuming that $P(B) \neq 0$
\[P(A|B) = \frac{P(A \cap B)}{P(B)}\] \[\Rightarrow P(A \cap B) = P(B). P(A|B)\] \[=P(A). P(B|A)\]Assuming that $P(A \cup B) \neq 0$,
\[P(A \cup B | C) = P(A|C) + P(B|C)\]Conditioning on multiple events
\[P(A\vert B,C) = \frac{P(A \space \cap \space B \vert C)}{P(B \vert C)}\]1.6 Independence
Events $E_1, E_2, …, E_n$ are independent if for every subset wih $k$ elements ($k \leq n$):
\[P(E_1, E_2, ..., E_k) = \prod_{i=1}^k P(E_i)\]Conditional Independent
